午後のひとときに、数学の図形問題を解いてみる。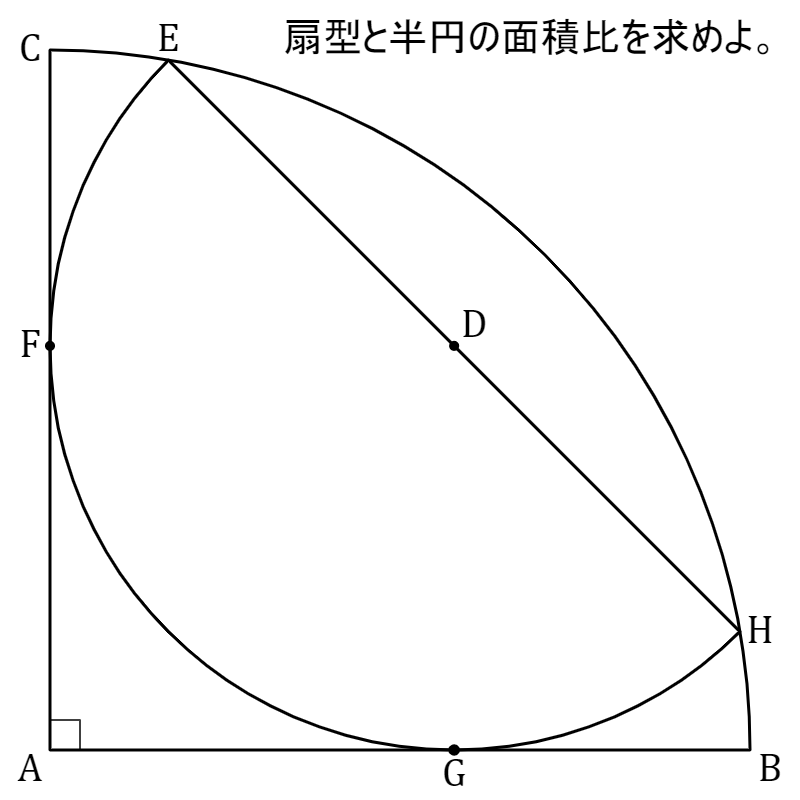
上記のように、仰角90˚の扇形に内接する半円がある。
扇形と半円の面積比を求めよ。
シンキングタ~イム
今回の問題は、長さが一つも示されていません。
ということは、どこかの長さを仮に決めて、そこからいろいろなところの長さを確定していって、最小的には面積比が求まるのだということです。
半円の半径を1としましょうか。
DE = DF = DG = DH =1
というわけで、DFとDGの補助線を引きます。
F、Gはそれぞれ、半円の弧と直線の接点なので、垂線の足となって、
∠DFA = ∠DGA = 90˚
となります。
∠CAB =90˚より、
四角形DFAGは正方形となります。
まだ補助線が足りません。
正方形DFAGの対角線ADを引きます。
最後に扇形の半径となるAHを引いて、補助線は終わりです。
半円は仰角90˚の扇形に内接していることから、
弧CE = 弧BH
であり、
点Dは線分EHの中点であるから、
AD ⊥ EH
ということが解る。
直角三角形ADHに着目すると、
DHは半円の半径、
AHは扇形の半径、
である。
1辺が1の正方形の対角線の長さは、
AD = √2
ピタゴラスの定理より、
AH = √3
今回の問題は面積比を問うてるので、
仰角90˚の扇形の面積は、πr2/4
半円の面積は、πr2/2
それぞれの半径を代入すると、
仰角90˚の扇形の面積:半円の面積 = 3π/4:π/2 = 3:2
答え 3:2
解が整数比で表せるのがいいですね。
面積比ではなくて、面積を求めさせても面白いかもしれませんね。
ではでは