午後のひとときに、算数、数学の問題を解答するよ。
問題
立方体を平面で2つの物体に切断したとき、
切断面としてあり得ないものをすべて選べ。
あり得るものは1つ以上の例を挙げ、
あり得ないものはあり得ないことを証明せよ。
- 正三角形
- 直角二等辺三角形
- 二等辺三角形(但し、正三角形、直角二等辺三角形を含まない)
- 直角三角形(但し、直角二等辺三角形を含まない)
- 三角形(但し、上記以外)
- 正方形
- 長方形(但し、正方形を含まない)
- 菱形(但し、正方形を含まない)
- 平行四辺形(但し、長方形、菱形を含まない)
- 等脚台形(但し、長方形を含まない)
- 台形(但し、長方形、菱形、平行四辺形、等脚台形を含まない)
- 凧形(但し、正方形、菱形を含まない)
- 四角形(但し、上記以外)
- 正五角形
- 五角形(但し、正五角形を含まない)
- 正六角形
- 六角形(但し、正六角形を含まない)
- 正n角形(但し、nは7以上)
- n角形(但し、nは7以上で、正n角形を含まない)
まずはサンプルをいくつか描いてみました。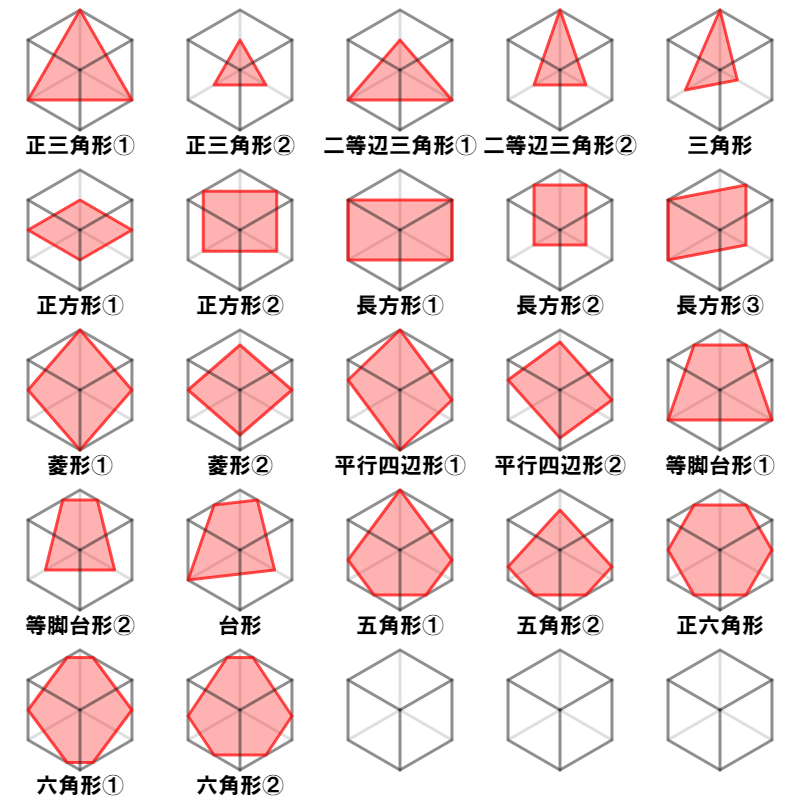
描けたグループ:
正三角形、二等辺三角形、三角形、正方形、長方形、菱形、平行四辺形、等脚台形、台形、五角形、正六角形、六角形
描けなかったグループ:
直角二等辺三角形、直角三角形、凧形、四角形、正五角形、正n角形、n角形
解説
まず、立方体を切断するにあたって、どのように考えるのが良いのか。
辺上を動く3点、但し立方体の同一面上には3点が存在しないものとする。
という点を考える。
立方体の同一面上に3点が存在すると、面を高さ0で薄く切断することになる。
これも正方形の答えではあるが、わざわざ切断された立体の体積が0になるケースは考えなくても良いだろう。
この3点が決まると、平面が決まり、切断面が確定します。
正三角形①
辺で隣り合わない、もしくは面で対角となる3頂点を選ぶ。
この3点を通る平面で切断すると、それぞれの辺は立方体の面の対角線となり等しく、正三角形となる。
正三角形②
正三角形は、なにも立方体の頂点だけで作られるわけではないという例。
二等辺三角形①
正三角形①の上の点を奥の辺を通って下方向へ移動すると、二等辺三角形となる。
二等辺三角形②
二等辺三角形①とは逆に、底辺の2点を奥へ平行に移動すると、二等辺三角形となる。
三角形
立方体奥の頂点に接する3辺上の各辺上に点を取る。
立方体奥の頂点からの距離がそれぞれ異なれば、正三角形でも二等辺三角形でも無い三角形となる。
ここまでが描けた三角形。
他の直角二等辺三角形、直角三角形が描けない理由は、立方体から直角を作りだすと、正方形か長方形となってしまうからです。
厳密に証明するには、正三角形①から二等辺三角形①を経由して、奥の頂点を限りなく下面に近づけていくことで、頂角が直角になろうとします。
しかし、頂角が直角になると、下面上の3点となり、切断面は三角形ではない。
よって、直角三角形は立方体の切断面とはなり得ない。
正方形①
立方体のどの面でも構わないが、上面か下面とすると、そこから水平に移動したとき、正方形となる。
3点は、正方形の4頂点のうちのいずれか3つであればよい。
正方形②
立方体のどの面にも平行でないケースも描けるという例です。
長方形①②③
いずれも、正方形②から、容易に考えることが可能であろう。
菱形①②
正方形①の左右の頂点を固定し、奥の頂点を上へ、手前の頂点を下へ、辺を通って移動すると、菱形となる。
正方形①→菱形②→菱形①
という変化で解るだろう。
平行四辺形①
菱形①の上下の頂点を固定し、左の頂点を上へ、右の頂点を下へ、辺を通って移動すると、平行四辺形となる。
平行四辺形②
平行四辺形①の左右の頂点を固定し、奥の頂点を下へ、手前の頂点を上へ、辺を通って移動したもの。
奥の頂点と左の頂点、手前の頂点と右の頂点、それらの高さが等しくなると、長方形となるので、高さが等しくない間は平行四辺形となる。
等脚台形①
長方形①の底辺を固定し、上辺を奥へ移動すると、等脚台形となる。
上辺を上奥の頂点まで移動すると正方形、更に奥の辺を下がると二等辺三角形へと変形する。
長方形①→等脚台形①→正三角形①→二等辺三角形①
等脚台形②
必ずしも立方体の頂点を選択する必要性はないという例。
台形
等脚台形①の左辺と等脚台形②の右辺より作られた台形。
上底と下底が平行で、左辺と右辺の長さが等しくなければ、等脚台形ではない台形を描くことが可能。
さて、ここまで挙げてきた四角形以外の四角形は作れないのはなぜか。
四角形を作るには、最低でも立方体の4面を通るように切断する必要がある。
どのように切断したとしても、上辺と下辺、または、左辺と右辺、どちらか一方または両方が平行となる。
これにより、平行という条件がない四角形は、立方体の断面にはなり得ない。
つまり、凧形(但し、正方形、菱形は含まない)、四角形(但し、上記を含まない)は、立方体の切断面とはなり得ない。
正六角形
立方体の同一面上に存在しない辺の中点を3つ選び、切断すると正六角形となる。
六角形①
正六角形の左右の頂点を固定し、上辺を奥へ、下辺を手前へ、面に沿って移動すると、六角形となる。
正六角形→六角形①→菱形①→菱形②→正方形①
のような変形となる。
六角形②
正六角形の下辺を固定し、上辺を奥へ、面に沿って移動すると、六角形となる。
五角形①②
正六角形→六角形②→五角形①→五角形②→
という変化により、五角形となる。
底辺は底面の手前側であれば頂点を通らなければ良い。
まず、五角形①、五角形②、どちらも線対称、同様に正五角形も線対称です。
つまり、正五角形が線対称であることから、存在するならば
五角形①→五角形②→
という変形の途中に出現する必要がある。
下辺の長さは下面に沿って平行移動することで調整は可能である。
証明のアプローチは色々考えられるが、五等辺五角形を考えてみる。
奥の頂点を頂角、下辺を底辺として、
頂角に接する2辺に着目すると、立方体の面の対辺を横切るので、立方体の辺の長さよりも長くなります。
仮に、底辺を底面に沿って平行に移動して、立方体の辺の長さよりも長くすると、
底辺に接する2辺が立方体の辺の長さよりも短くなる。
これにより、立方体の切断面で五等辺を作ることが出来ない。
よって正五角形は立方体の切断面になり得ない。
正n角形、n角形がなり得ないのは、立方体の面の数が6より、最大でも6辺までなので六角形までであり、7辺以上を作ることが出来ない。
いかがでしょうか。
手元に紙と鉛筆などがあるならば、等角投影法などで描くことで、イメージを膨らませやすい。
ただ、リアリティを追求して透視図法で描くと、五角形を正しく描くことに苦労するだろうから、透視図法は辞めたほうがいい。
CGなどで勝手にやってくれるような環境があるならば、透視図法でも全く問題ないだろう。
まぁ、そういう環境を作ったり用意したりするのは手間がかかるだろう。
もし、手元に紙と鉛筆がなかったら、頭の中だけで想像出来るだろうか。
日頃からの鍛錬が必要だろうな。
ではでは