sin18˚, cos72˚, cos36˚, sin54˚を簡単に求める方法

随分前にオイラーの公式を使って、極座標で18度系を求めたんだよね。



上記の方法は、高校の理系クラスレベルになっているので、小中学生、文系には厳しい話しです。

こんな難しいことをやらなくても、sin18˚、cos72˚、cos36˚、sin54˚を求める方法がありますよということを紹介します。

レベル的には中学生レベル、高校受験レベル、高校文系クラスレベルでしょうか。
小学生でも三角形の辺の比はやるので、小学生でも理解出来るレベルかもしれません。

図形的なアプローチをします。
頂角を36˚、底角を72˚の二等辺三角形を描きます。（黒線、黒文字）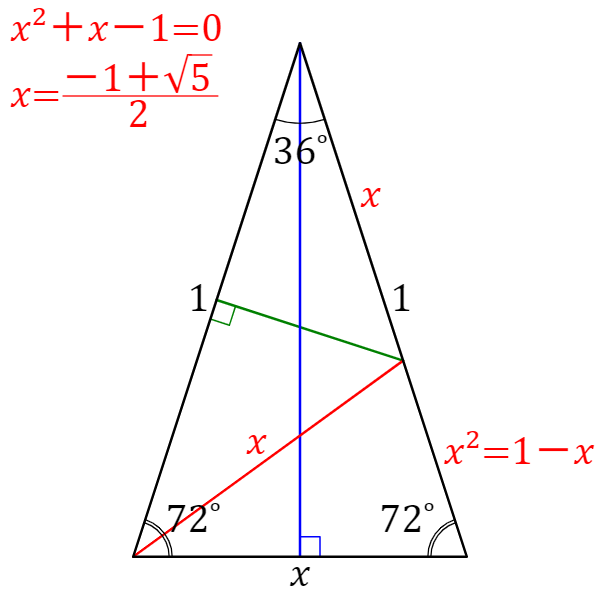



辺の比は、1：1：x とします。
底角のどちらを二等分線（赤線）を引きます。
すると、72˚を半分にしているので、36˚となって、新たに出来た2つの三角形も二等辺三角形であることがわかりますね。
下側の小さな二等辺三角形の斜辺は、大きな二等辺三角形の底辺、つまり x ですね。
頂角が36˚で等しいので、相似ですね。
ですので、下側の小さい二等辺三角形の底辺の長さを比で求めると、
1：1：x＝x：x：x²
つまり x² となります。

また、赤線で分割された残りのほうも、底角が36˚の二等辺三角形ですから、斜辺の長さが等しく x となりますので、
下側の小さい二等辺三角形の底辺の長さは、1-xと表わせ、
x²=1-x
となり、移項すると、
x²+x-1=0
二次方程式の解の公式で解くと、
x=(-1±√5)/2
となり、xは辺の長さなので正で、
x=(-1+√5)/2
と定まります。

さて、タイトルの、sin18˚、cos72˚、cos36˚、sin54˚を求めるには、図の辺の長さが求まっていますので、
青線や緑線で二等分して、三角比で考えるだけです。

sin18˚=cos72˚=(x/2)/1=x/2=(-1+√5)/4
cos36˚=sin54˚=(1/2)/x=(1/2)/((-1+√5)/2)=1/(-1+√5)=(1+√5)/4

一番難しいところでも二次方程式の解の公式ですから、随分と簡単に求まりましたね。
残りの18度系は、ピタゴラスの定理で青線や緑線の高さを求めたり、三角関数の公式とかやっていけば、求まりますね。


ではでは