最近、何気にちょこちょこと、音楽関連の話しをブログに書いている。
最近だと、サザンオールスターズのコード進行とか、テーマは数楽だったけど、50番目のメルセンヌ素数が発見されるにて、メルセンヌさんの音楽に関する功績を書いている。
別に音楽畑出身でもなければ、音楽理論も解ってはいない。
もしかすると、音楽畑出身でも、この辺の理論については解かっていない人もいるのかもしれない。
理論とか苦手な人は多いですからね。
というわけで、Excelを使って、解りやすい数値を出してみようかと思う。
まずは、ピタゴラス音律。
なんで、音楽のことなのに、数学者のピタゴラスが出て来るの?
というところだろうか。
メルセンヌも数学者であるが、音楽に関する功績もあると書いたとおり、ピタゴラスも音楽に関する功績があるのです。
ピタゴラスは紀元前582年~紀元前498年の数学者、哲学者である。
私の拙い歴史の知識だと、神武天皇が…、紀元前660年だったから、神話のレベルの時代背景ですよね。
そんな時代に音楽の基礎となる理論を確立したわけです。
では、ピタゴラス音律をExcelを使って計算してみましょう。
表1
表1の作り方
A13セルに、
=2^10
と入力すると、1024となったかと思います。
この表は、右へ行くと3倍、左へ行くと1/3倍、上へ行くと2倍、下へ行くと1/2倍、というように作りたい。
B13セルに、
=A13*3
と入力し、セルの右下の■をマウスでドラッグして、M13まで持っていきます。
これで、13行の作業はおしまい。
続いて、A12セルに、
=A13*2
と入力し、セルの右下の■をマウスでドラッグして、A3まで持っていきます。
同様の作業をG12セルまで、上記表の様に行います。
続いて、M14セルに、
=M13/2
と入力し、セルの右下の■をマウスでドラッグして、M23まで持っていきます。
同様の作業をM14セルまで、上記の表の様に行います。
これらの数値は、私が適当に作った周波数のサンプルです。
G列の、1492992、746496、373248、仮に、この列を音階D、和名ならレの音とします。
周波数が2倍になると、1オクターブ高くなる。
周波数が1/2倍になると、1オクターブ低くなる。
これは、どの列でもその様になっています。
ピタゴラス音階では、完全五度と完全四度を使って、音階を考えます。
右へ行くのは完全五度、左へ行くのは完全四度。
右へ行くと3倍、左へ行くと1/3になるようにしてあります。
さて、このデータをすべてを使ってもいいのですが、必要なところ、上記画像ではオレンジ色の部分だけを別セルに取りましょう。
A25セルに、
=MAX(A3:A13)
と入力し、セルの右下の■をマウスでドラッグして、G25まで持っていきます。
A26セルに、
=A25/2
と入力し、セルの右下の■をマウスでドラッグして、G26まで持っていきます。
G27セルに、
=MIN(G13,G23)
と入力し、セルの右下の■をマウスでドラッグして、M27まで持っていきます。
H26セルに、
=H27*2
と入力し、セルの右下の■をマウスでドラッグして、M26まで持っていきます。
1行、2行を入力して出来上がり。
=2^10
と入力すると、1024となったかと思います。
この表は、右へ行くと3倍、左へ行くと1/3倍、上へ行くと2倍、下へ行くと1/2倍、というように作りたい。
B13セルに、
=A13*3
と入力し、セルの右下の■をマウスでドラッグして、M13まで持っていきます。
これで、13行の作業はおしまい。
続いて、A12セルに、
=A13*2
と入力し、セルの右下の■をマウスでドラッグして、A3まで持っていきます。
同様の作業をG12セルまで、上記表の様に行います。
続いて、M14セルに、
=M13/2
と入力し、セルの右下の■をマウスでドラッグして、M23まで持っていきます。
同様の作業をM14セルまで、上記の表の様に行います。
これらの数値は、私が適当に作った周波数のサンプルです。
G列の、1492992、746496、373248、仮に、この列を音階D、和名ならレの音とします。
周波数が2倍になると、1オクターブ高くなる。
周波数が1/2倍になると、1オクターブ低くなる。
これは、どの列でもその様になっています。
ピタゴラス音階では、完全五度と完全四度を使って、音階を考えます。
右へ行くのは完全五度、左へ行くのは完全四度。
右へ行くと3倍、左へ行くと1/3になるようにしてあります。
さて、このデータをすべてを使ってもいいのですが、必要なところ、上記画像ではオレンジ色の部分だけを別セルに取りましょう。
A25セルに、
=MAX(A3:A13)
と入力し、セルの右下の■をマウスでドラッグして、G25まで持っていきます。
A26セルに、
=A25/2
と入力し、セルの右下の■をマウスでドラッグして、G26まで持っていきます。
G27セルに、
=MIN(G13,G23)
と入力し、セルの右下の■をマウスでドラッグして、M27まで持っていきます。
H26セルに、
=H27*2
と入力し、セルの右下の■をマウスでドラッグして、M26まで持っていきます。
1行、2行を入力して出来上がり。
さて、この表をみると、A♭とG♯のそれぞれの音が食い違っていることに気がつくかと思います。
そもそも、ピタゴラス音階は、数学的にいうところの、有理数の範疇の話しなので、音階を対数的に12等分した平均律、数学的にいうところの、無理数の範疇ではありません。
とりあえず、A♭は使わず、B25からM27までの2オクターブ分の周波数サンプルを使います。
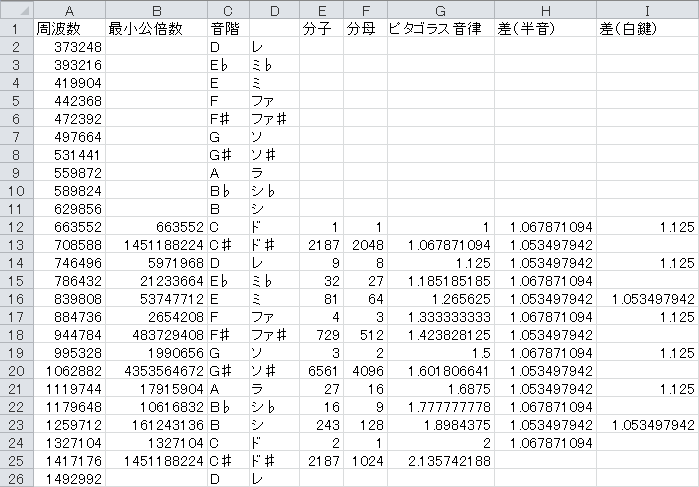
表2
表2の作り方
表1のB25からM27を選択し、Ctrl + Cを押し、コピーします。
別シートのA2セルにカーソルを合わせて、Alt + V、E、Sと順番にキー操作します。
B12からB14を選択し、Ctrl + X、B9でEnter
C8から14を選択し、Ctrl + X、C22でEnter
A2からA28を選択し、Alt + D、S、と順番にキー操作します。
A1セルに周波数と入力
B1セルに最小公倍数と入力
とりあえず、ドから1オクターブ上のドまでのデータを作りたいので、
B12セルに、
=LCM(A$12,A12)
と入力し、セルの右下の■をマウスでドラッグして、B25まで持っていきます。
C列、D列、1行は、表2の通り
E12セルを、=B12/A$12
F12セルを、=B12/A12
G12セルを、=E12/F12
とそれぞれ入力
E12からG12を選択し、右下の■をマウスでドラッグして、G25まで持っていきます。
H12セルに、
=G13/G12
と入力し、セルの右下の■をマウスでドラッグして、H24まで持っていきます。
I12セルに、
=G14/G12
と入力し、Ctrl + C
I14、I17、I19、I21、それぞれで、Ctrl + V
I16セルに、
=H16
と入力し、Ctrl + C
I23で、Ctrl + V
完成です。
別シートのA2セルにカーソルを合わせて、Alt + V、E、Sと順番にキー操作します。
B12からB14を選択し、Ctrl + X、B9でEnter
C8から14を選択し、Ctrl + X、C22でEnter
A2からA28を選択し、Alt + D、S、と順番にキー操作します。
A1セルに周波数と入力
B1セルに最小公倍数と入力
とりあえず、ドから1オクターブ上のドまでのデータを作りたいので、
B12セルに、
=LCM(A$12,A12)
と入力し、セルの右下の■をマウスでドラッグして、B25まで持っていきます。
C列、D列、1行は、表2の通り
E12セルを、=B12/A$12
F12セルを、=B12/A12
G12セルを、=E12/F12
とそれぞれ入力
E12からG12を選択し、右下の■をマウスでドラッグして、G25まで持っていきます。
H12セルに、
=G13/G12
と入力し、セルの右下の■をマウスでドラッグして、H24まで持っていきます。
I12セルに、
=G14/G12
と入力し、Ctrl + C
I14、I17、I19、I21、それぞれで、Ctrl + V
I16セルに、
=H16
と入力し、Ctrl + C
I23で、Ctrl + V
完成です。
表2の見方
周波数サンプルは、私が最小公倍数を求めるため、良い意味で適当な2のべき乗の整数から他を作り上げたにすぎません。
実際の音階の周波数の話しは別です。
分子、分母、ピタゴラス音律
ピタゴラス音律は、先にも書いたが、数学的にいうところの、有理数の範疇である。
つまり、分母、分子が整数の比で表せます。
表のピタゴラス音律は、Cを1としたときに、他の音は分数でいくつということです。
完全五度とは、3:2、つまりCを3/2倍=1.5倍すると、Gになるよということ。
完全四度とは、4:3、つまりCを4/3倍すると、Fになるよということ。
これを基準にした音律、音階なわけですね。
この比率は、何らかの打楽器とか、弦楽器とか、物理的なものの長さを、2倍にしたり、3倍にしたり、半分にしたり、1/3にしたりとかからヒントを得たんだと思う。
差(半音)の列をみてみると、
表において、1.067871094と1.053497942の2種類の比率がみえる。
正確を期すため分数にすると、
1.067871094 = 2187/2048
1.053497942 = 256/243
です。
この2種類を掛け合わせると、全音の1.125になります。
この2種類の半音があることで、移調とか、転調とか、そういうことには向かないということなのだろうけど、時代が紀元前の話しですので、これくらいの理論でも十分だったのかもしれません。
このピタゴラス音律に対して、12平均律を確立したのが、メルセンヌです。
メルセンヌも数学者であり、物理学者であり、哲学者であり、音楽理論にも貢献している。
メルセンヌの時代は、西暦1588~1648ですので、ピタゴラスからみて2000年以上の隔たりがあります。
12平均律とは、簡単に言えば、1オクターブを対数的に12等分するということ。
2^(1/12)という無理数の比です。
実際には1オクターブを20000000:1000000の比として、その間の近似値で埋めていきました。

表2'
表2に、純正律、平均律を計算してみましょう。
N12セルに、
=2^(1/12)
を入力。
N13セルに、
=N12*2^(1/12)
と入力し、セルの右下の■をマウスでドラッグして、N24まで持っていきます。
H12からI24までを選択し、Ctrl + C、O12セルでEnter
純正律は、J列の分子、K列の分母を、数値的に入力し、L列やM列を、他の律と同様に計算します。
=2^(1/12)
を入力。
N13セルに、
=N12*2^(1/12)
と入力し、セルの右下の■をマウスでドラッグして、N24まで持っていきます。
H12からI24までを選択し、Ctrl + C、O12セルでEnter
純正律は、J列の分子、K列の分母を、数値的に入力し、L列やM列を、他の律と同様に計算します。
表2'の見方
平均律は、1.059463094という値で示された通り、均一の値ですね。
見た目は有限小数ですが、実際は2^(1/12)ですね。
どこの半音の差も等しいので、、移調、転調がスムーズに行えます。
純正律は、白鍵の部分だけのデータの入力に留めましたです。
白鍵の列をみると、
全音が、1.125と1.111111111の2種類あることが解ります。
EからF、BからCの半音は共に、1.066666667ですね。
これも正確を期すため分数にすると、
1.125 = 9/8
1.111111111 = 10/9
1.066666667 = 16/15
です。
ピタゴラス音律のとき、全音は1.125の1種類だったのに、半音は2種類ありました。
この考えでいくと、純正律の半音はもっと複雑になり、もっと種類が出来てくるのでしょう。
純正律は、ピタゴラス音律と平均律の間で、出来るだけ単純な分数にしたかった。
どのような根拠で、このような分数を持ってきたかというと、長三和音の比が4:5:6という単純な比になるようにということ。
C:G:E=(1/1):(5/4):(3/2)=4:5:6
F:A:C=(4/3):(5/3):(2/1)=4:5:6
G:B:D=(3/2):(15/8):(9/4)=12:15:18=4:5:6
今回紹介した音楽の理論は、Excelで計算出来るような、数学者が確立した理論ということです。
まぁ、これを知らなければ、音楽を楽しむことは出来ないというわけではありません。
しかし、音大などの音楽系の大学に進んでまで、音楽を極めようと考えている人にとっては、実践以外にも、こういった理論も、ある程度知っておく必要があるのでしょうね。
でも、畑違いの数学の話しですから、かなり厳しく辛いとは思いますね。
ではでは