tan xのマクローリン展開をやらないの？

sin xとcos xのマクローリン展開のアニメGIFの記事が、なぜか人気がある。

なんで、tan xのマクローリン展開をやらないの？と自分へと問いかけてみる。

出来なくはないんだけど、高次方程式の各項の係数の表現が、sin xやcos xのように簡潔に表せないからである。

そこを簡潔に表せたら、やってもいいかな。

係数の分母は階乗になるんだけど分子が面倒なんです。

f(x) = tan(x)

f'(x) = (tan(x))' = 1/cos²(x) = 1 + tan²(x)
f'(0) = 1

f''(x) = (tan(x))'' = (1 + tan²(x))' = (1)' + (tan²(x))' = (0 + 2tan(x))(1 + tan²(x)) = 2tan(x) + 2tan³(x)
f''(0) = 0

f'''(x) = (2tan(x) + 2tan³(x))'(1 + tan²(x)) = (2 + 6tan(x))(1 + tan²(x)) = 2 + 8tan²(x) + 6tan⁴(x)
f'''(0) = 2

f''''(x) = (2 + 8tan²(x) + 6tan⁴(x))'(1 + tan²(x)) = (16tan(x) + 24tan³(x))(1 + tan²(x)) = 16tan(x) + 40tan³(x) + 24tan⁵(x)
f''''(0) = 0

f'''''(x) = (16tan(x) + 40tan³(x) + 24tan⁵(x))'(1 + tan²(x)) = (16 + 120tan²(x) + 120tan⁴(x))(1 + tan²(x)) = 16 + 136tan²(x) + 240tan⁴(x) + 120tan⁶(x)
f'''''(0) = 16

f''''''(x) = (16 + 136tan²(x) + 240tan⁴(x) + 120tan⁶(x))'(1 + tan²(x)) = (272tan(x) + 960tan³(x) + 720tan⁵(x))(1 + tan²(x)) = 272tan(x) + 1232tan³(x) + 1680tan⁵(x) + 720tan⁷(x)
f''''''(0) = 0

f'''''''(x) = (272tan(x) + 1232tan³(x) + 1680tan⁵(x) + 720tan⁷(x))'(1 + tan²(x)) = (272 + 3696tan²(x) + 8400tan⁴(x) + 5040tan⁶(x))(1 + tan²(x)) = 272 + 3968tan²(x) + 12096tan⁴(x) + 13440tan⁶(x) + 5040tan⁸(x)
f'''''''(0) = 272

7階微分まで手でやってみたが、面倒だな。
まぁ、プログラムでやるならば問題はないけど。

偶数階微分にx=0を代入すると0になるので、奇数階微分のx=0の値が分子に来て、分母は奇数階乗です。

tan x = (1/1!)x + (2/3!)x³ + (16/5!)x⁵ + (272/7!)x⁷ + …

まぁ、分子の計算式を書かないならば、どうにか出来そうな気がしてきたな。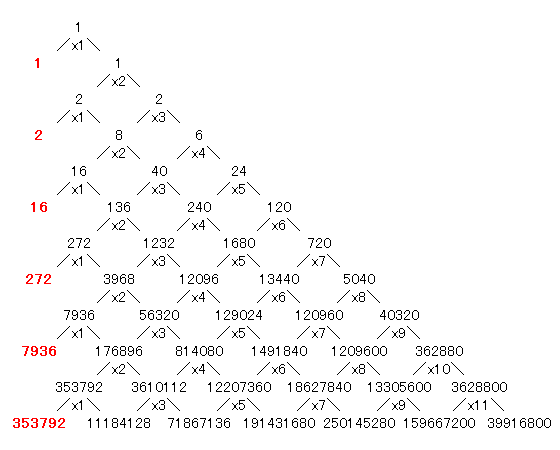



こんなような計算になるだろうか。


ではでは